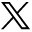Advertisement

AJNR Awards, New Junior Editors, and more. Read the latest AJNR updates

OtherPHYSICS REVIEW

Diffusion Tensor MR Imaging and Fiber Tractography: Theoretic Underpinnings

P. Mukherjee, J.I. Berman, S.W. Chung, C.P. Hess and R.G. Henry
American Journal of Neuroradiology April 2008, 29 (4) 632-641; DOI: https://doi.org/10.3174/ajnr.A1051

Abstract

SUMMARY: In this article, the underlying theory of clinical diffusion MR imaging, including diffusion tensor imaging (DTI) and fiber tractography, is reviewed. First, a brief explanation of the basic physics of diffusion-weighted imaging (DWI) and apparent diffusion coefficient (ADC) mapping is provided. This is followed by an overview of the additional information that can be derived from the diffusion tensor, including diffusion anisotropy, color-encoded fiber orientation maps, and 3D fiber tractography. This article provides the requisite background for the second article in this 2-part review to appear next month, which covers the major technical factors that affect image quality in diffusion MR imaging, including the acquisition sequence, magnet field strength, gradient amplitude and slew rate, and multichannel radio-frequency coils and parallel imaging. The emphasis is on optimizing these factors for state-of-the-art DWI and DTI based on the best available evidence in the literature.

Diffusion MR imaging of the brain was first adopted for use in clinical neuroradiology during the early 1990s and was found to have immediate utility for the evaluation of suspected acute ischemic stroke. Since that time, enormous strides forward in the technology of diffusion imaging have greatly improved image quality and enabled many new clinical applications. These include the diagnosis of intracranial pyogenic infections, masses, trauma, and vasogenic-versus-cytotoxic edema. Furthermore, the advent of diffusion tensor imaging (DTI) and fiber tractography has opened an entirely new noninvasive window on the white matter connectivity of the human brain. DTI and fiber tractography have already advanced the scientific understanding of many neurologic and psychiatric disorders and have been applied clinically for the presurgical mapping of eloquent white matter tracts before intracranial mass resections.

This 2-part review explores the current state of the art for the acquisition and analysis of clinical diffusion imaging, including DTI and fiber tractography. This first article begins with an explanation of the basic physics and underlying theory of diffusion-weighted imaging (DWI) and apparent diffusion coefficient (ADC) mapping. This is followed by an overview of the additional information that can be derived from the diffusion tensor, including diffusion anisotropy, color-encoded fiber-orientation maps, and 3D fiber tractography. This article provides the necessary background for the second article, which focuses on the major technical factors that affect image quality in diffusion imaging, with an emphasis on optimizing these factors for state-of-the-art DWI and DTI based on the best available evidence in the literature.

Theoretic Underpinnings of Diffusion Imaging

Brownian Motion and Tissue Ultrastructure

Diffusion, also known as “Brownian motion,” refers to constant random microscopic molecular motion due to heat. At a fixed temperature, the rate of diffusion can be described by the Einstein equation1: Math1), where <r2> refers to the mean squared displacement of the molecules, t is the diffusion time, and D is the diffusion constant, a constant of proportionality for the particular substance being measured. In clinical diffusion imaging, the type of diffusion being investigated is water self-diffusion, meaning the thermal motion of water molecules in a medium that itself consists mostly of water.2–5 The diffusion constant, typically expressed in units of square millimeters per second, relates the average displacement of a molecule over an area to the observation time, with higher values of this constant indicating more mobile water molecules. The ADC is the diffusion constant measured in the clinical setting, reflecting the limitation that in vivo diffusion cannot be separated from other sources of water mobility, such as active transport, flow along pressure gradients, and changes in membrane permeability.

Imaging molecular water diffusion confers the ability to probe the microstructural properties of biologic tissues. The typical diffusion times used for clinical DWI are 10–50 ms, corresponding to average molecular displacements on the order of 10 μm. This microscopic spatial scale is in the same range as that of cellular dimensions. This sensitivity to cellular processes has been exploited clinically for improving the detection of acute cerebral ischemia,4, 6–10 distinguishing vasogenic from cytotoxic edema,11–16 identifying foci of axonal shearing injury after acute head trauma,17–19 characterizing cellularity in brain tumors,20–27 discriminating between metastases and gliomas22, 27 and between tumor recurrence and postsurgical injury,28 differentiating pyogenic abscesses from tumors,29–31 and for the noninvasive mapping of white matter connectivity by using the diffusion tensor model,32–36 among other applications.

Stejskal-Tanner Diffusion Encoding

A diffusion-weighted pulse sequence is constructed by the addition of a pair of diffusion-sensitizing gradients, also known as motion-probing gradients, to a T2-weighted spin-echo sequence. The diffusion gradients are applied along the same directional axis both before and after the 180° refocusing pulse (Fig 1). This is known as Stejskal-Tanner diffusion encoding.37 Molecular motion thus results in loss of signal intensity due to incomplete rephasing of water proton spins, which change position between and during the applications of the 2 diffusion-sensitizing gradients. This diffusion-weighted contrast can be fit to an exponential model: Math2).

Fig 1.
Fig 1.

Pulse sequence diagram for a diffusion-weighted acquisition shows that 2 diffusion-sensitizing gradients (dark gray) are added to a spin-echo sequence, 1 before and 1 after the 180° refocusing pulse. The diffusion-weighting factor b depends on the amplitude of the diffusion gradient (G), the duration of each diffusion gradient (δ), and the interval between the onset of the diffusion gradient before the refocusing pulse and that following the refocusing pulse (Δ). RF indicates radiofrequency pulses; Gz, gradient pulses.

In the above expression, Si is the diffusion-weighted signal intensity observed at a given voxel with the diffusion-sensitizing gradients applied along direction i, S0 is the signal intensity at the same voxel measured without diffusion-sensitizing gradients, and ADCi is the ADC in the i direction. Within the exponential term, the b factor is a measure of diffusion-weighting that is a function of the strength, duration, and temporal spacing of the diffusion-sensitizing gradients, assuming rectangular gradient pulses: Math3) where γ is a physical constant known as the gyromagnetic ratio, G is the amplitude of the diffusion gradient typically measured in milliteslas per meter, δ is the duration of each diffusion gradient in milliseconds, and Δ is the interval between the onset of the diffusion gradient before the refocusing pulse and that after the refocusing pulse, measured in milliseconds (Fig 1). The units of b are seconds per square millimeter, reciprocal to the units of ADC. It can be seen from equation 2 that raising b increases the degree of diffusion-weighting (ie, the loss of signal intensity Si along direction i produced by application of the diffusion gradients). From equation 3, it is apparent that boosting the gradient amplitude G and the gradient duration δ are the most effective ways of increasing the diffusion-weighting, due to the quadratic dependence of b on these 2 parameters. Typical values of b used in clinical applications range from 600 to 1500 seconds per square millimeter. The lowest values of b are used for imaging of fetuses in utero or premature neonates, due to the very high ADC values of these structurally immature brains.38, 39 The highest b factors have been advocated for hyperacute stroke imaging in adults at 1.5T, to maximize sensitivity to the often subtle reductions in ADC in this very early stage of cerebral ischemia,40, 41 though a recent 3T study42 found no benefit of b = 1500 s/mm2 DWI for stroke detection compared with the traditional adult b-value of 1000 s/mm2.

Diffusion-Weighted Image Contrast and ADC Calculation

In equation 2, ADCi is the ADC of water along the direction of the diffusion-sensitizing gradient. Higher ADC values, reflecting greater rates of water diffusion in the tissue under investigation, result in lower signal intensity Si in the diffusion-weighted image (Fig 2). Conversely, reduced ADC values result in higher observed signal intensity on DWI. The direct calculation of ADC values has assumed considerable clinical importance because of the T2-weighting inherent in the long TE of a DWI pulse sequence: Math4) where k is a proportionality constant and T2 is the transverse relaxation time of the interrogated tissue. Hence, T2 prolongation within pathologic tissues may cause DWI signal hyperintensity, even in the absence of reduced ADC values. This T2 shinethrough effect renders DWI hyperintensity less specific for clinical diagnosis than decreases of ADC that are confirmed on an ADC map (Fig 3). Conversely, decreases in T2 may mask a true reduction in ADC values; this phenomenon has been referred to as “T2 blackout”.43 T2 blackout may be at least in part responsible for the relatively low sensitivity of DWI signal intensity compared with ADC maps for the detection of acute hypoxic-ischemic injury in neonatal white matter because such lesions typically reduce the very long T2 relaxation times of white matter in neonates. However, T2 effects can also be beneficial: The “lightbulb” brightness of DWI signal intensity in acute infarcts of the adult brain is caused by the multiplicative effect of T2 prolongation and reduced ADC (equation 4). Therefore, DWI has better sensitivity than ADC maps for small acute ischemic lesions in children beyond infancy and in adults.

Fig 2.
Fig 2.

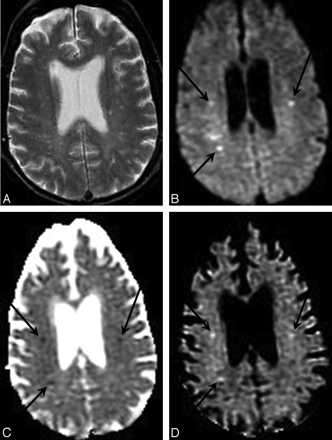
DWI enables more sensitive and specific diagnosis of acute cerebral ischemia in a case of embolic infarcts due to endocarditis. A, Conventional spin-echo T2-weighted image shows only nonspecific white matter foci of signal hyperintensity. B, Combined DWI image at the same axial level reveals 3 punctuate hyperintense white matter lesions (arrows) that are suggestive of embolic infarcts. C, Corresponding ADC map confirms that there is reduced diffusion in these lesions (arrows), consistent with acute ischemia. D, Attenuation coefficient image, also known as the exponential diffusion image, shows these lesions as remaining hyperintense (arrows). This demonstrates that the hyperintensity on the combined DWI image is not due to T2 shinethrough artifact.

Fig 3.
Fig 3.

T2 shinethrough artifact in DWI. A, T2-weighted fluid-attenuated inversion recovery image shows numerous nonspecific periventricular and subcortical hyperintense foci, as well as a larger wedge-shaped region of hyperintensity in the right parietal lobe suggestive of infarct. B, Combined DWI image at the same axial level reveals that the right parietal abnormality is hyperintense, suggesting acute ischemia. C, Corresponding ADC map demonstrates elevated mean diffusivity within the abnormal region, consistent with chronic infarction. D, Low signal intensity within the lesion on the attenuation coefficient image confirms that the DWI signal-intensity hyperintensity is due to T2 shinethrough and does not reflect reduced diffusion as would be seen in an acute infarct.

ADC values may be calculated from DWI by solving for ADC in equation 2: 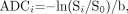Math5) where ln is the natural logarithm. The signal intensity S0 in the absence of a diffusion-sensitizing gradient can be derived from an image acquired at b = 0 s/mm2. In general, ADC maps can be derived from a set of diffusion-weighted images acquired at a high b factor and a second set of images acquired with a low b factor, which can be zero. This only applies in the range of b- values used clinically, because for b-values greatly exceeding 1000 s/mm2, DWI signal intensity Si no longer conforms to the monoexponential relationship with b described in equation 2.44, 45

Another popular way of examining diffusion images without the contaminating influence of T2 effects is with an attenuation coefficient (AC) map, also known as the exponential diffusion-weighted image,46 the exponential image, or the attenuation factor map (Fig 2). The AC map can be computed by dividing the diffusion-weighted image Si by the T2-weighted b = 0 s/mm2 image S0. This yields Math6).

Note from the last expression, compared with equation 4, that only the diffusion-related exponential term remains, eliminating the T2-weighting effects. Like DWIs, areas of reduced diffusion appear bright on AC maps and areas of elevated diffusion appear dark. This is the opposite of the contrast polarity of ADC images. However, like ADC maps, AC maps remain less sensitive than DWI signal hyperintensity for detecting small acute infarcts because they lack the multiplicative effect of T2 prolongation combined with reduced diffusion that produces the “lightbulb” effect on DWI.

Isotropy, Anisotropy, and Rotational Invariance

In isotropic diffusion, molecular motion is equal in all directions. Pure water at body temperature demonstrates isotropic diffusion, with an ADC of approximately 3.0 × 10−3 mm2/s. In the human brain, isotropic diffusion may be found in the CSF spaces, except in areas of bulk flow such as the jets emanating from the foramina of Monro or through the cerebral aqueduct. Due to its complex microarchitecture, the gray matter of the cerebral cortex in adults is also thought to exhibit isotropic diffusion at the clinical range of b-values,33, 47 though some studies differ.48 When diffusion is isotropic, the choice of direction for the diffusion-sensitizing gradient is not important because ADCi is identical for all directions i.

In anisotropic diffusion, molecular mobility is not equal for all directions. White matter tracts with tightly packed coherently oriented fiber bundles hinder water displacement perpendicular to the direction of the fibers, resulting in larger ADCi values parallel to the tracts rather than orthogonal to them.49 Hence, more than 1 diffusion-encoding direction is required to characterize regions of anisotropic diffusion. If only a single diffusion direction was probed, interpretation of the DWIs would be complicated by variable signal intensity in white matter tracts, depending on their orientation relative to the direction of the diffusion gradient, which could also be affected by changes in the orientation of the patient's head. Although this anisotropy can be exploited in DTI, to be discussed in detail below, it is not desirable for routine clinical DWI. To avoid this problem, one can compute parameters with the property of rotational invariance from the original DWI data because these measures mathematically eliminate any directional dependence that might confuse clinical interpretation.

Computation of commonly used rotationally invariant measures, such as the geometric mean DWI and the trace ADC, requires at least 4 separate image acquisitions: 1 without diffusion-sensitizing gradients (b = 0 s/mm2), labeled S0, and 3 probing motion along 3 mutually orthogonal directions, labeled S1, S2, and S3, respectively. The DWIs submitted to the radiologist for interpretation are not typically the sets of unidirectional DWIs S1, S2, and S3 but rather the rotationally invariant geometric mean computed from these 3 image sets, also known as the “isotropic DWI” or the “combined DWI”: Math7), where ADC1, ADC2, and ADC3 are the ADCs along the directions of the 3 diffusion-sensitizing gradients and, in the final expression, ADC = (ADC1 + ADC2 + ADC3)/3. This last variable, ADC, is the average of the ADCi values along the 3 orthogonal directions and is also rotationally invariant. It is variously known as the mean diffusivity, the trace ADC, Dav, or, simply, the ADC. Henceforth in this discussion, as is typical in the clinical setting when the acronym ADC is used, it will refer to this averaged value.

Isotropic DWI and trace ADC maps can be constructed from more than 3 diffusion-encoding directions. However, it is preferable that the diffusion-encoding directions not be collinear (ie, pointing in opposite directions along the same axis) and that they be as widely distributed in 3D space as possible. This latter condition is satisfied by mutual orthogonality in the case of 3 diffusion-encoding directions. Diffusion along 1 direction cannot be distinguished from diffusion in the polar opposite direction by Stejskal-Tanner diffusion encoding, a property known as “antipodal symmetry”. Therefore, 2 collinear diffusion-sensitizing gradients do not contribute independent information; hence, collinearity should be avoided in DWI acquisitions.

ADC Mapping of Healthy Human Brain and of Cerebral Pathology

In the healthy adult brain at the clinical range of b-values (<1500 s/mm2), the ADC of gray and white matter is very similar, such that DWI has little intrinsic gray-white matter contrast. Any gray-white contrast observed is primarily due to underlying differences in T2 (ie, the contrast of the b = 0 s/mm2 component of the image). Measured mean diffusivities in adult brain in vivo are 0.67–0.83 × 10−3 mm2/s for gray matter and 0.64–0.71 × 10−3 mm2/s for white matter.33 This differs from neonates and children, in whom ADC is initially very high at term gestational age, approximately 50% greater in rapidly developing gray matter structures such as thalamus and basal ganglia, and more than twice as high in slowly maturing lobar white matter regions.38, 39 Normal ADC values drop steeply during the first 2 years of postnatal life, during which time the initially higher ADC in most white matter becomes more equal to that in gray matter.50, 51 ADC values continue to decrease more gradually throughout childhood, adolescence, and young adulthood, with variable rates of decline that reflect heterogeneity in the speed of maturation in different parts of the brain.50–56 Conversely, in the healthy aging brain, mild increases in average brain ADC values may be seen with advancing age beyond 40 years, especially in white matter.57–62

Most types of pathology in the human brain cause increases of ADC values. Causes of abnormally reduced ADC in the human brain are less numerous, often allowing a more specific diagnosis. The most common ones are acute cerebral ischemia and other causes of cytotoxic edema, such as status epilepticus and hypoglycemia. The conventional explanation for reduced ADC in acute ischemia is that energetic failure leads to membrane permeability changes, resulting in cellular swelling and decreased volume and increased tortuosity of the extracellular space.63 However, this remains controversial because biophysical evidence has been presented that extracellular ADC and intracellular ADC are both reduced in acute cerebral ischemia, with the major contribution arising from the intracellular space.64

The viscosity of purulent material also reduces diffusion below that of the surrounding brain or CSF spaces. In vitro measurements of ADC values in pus indicate that viable cell attenuation is the most important determinant of hindered diffusion in pus.65 Hence, infectious etiologies for intracranially reduced diffusion include pyogenic abscess,29, 30 subdural or epidural empyema,66 and intraventricular empyema.67 Similarly, low ADC values due to hindered water motion also produce very bright signal intensity on DWI within extra-axial epidermoid masses68, 69 and within acute clotted hematomas, except in T2 dark hematomas due to T2 blackout.43 Highly cellular tumors, especially those with high nuclear-to-cytoplasmic ratios, can show reduced diffusion. Examples include the entire class of “small round blue cell tumors” such as lymphoma,25 neuroblastoma,70 and primitive neuroectodermal tumors such as medulloblastoma.23, 71 There have been case reports of brain metastases with restricted diffusion, even those without intralesional hemorrhage.72 Reduced diffusion has been described in the acute phase of primary demyelinating diseases,73, 74 metabolic disorders,74, 75 and toxic exposures.76–78 Rare causes of reduced ADC include Creutzfeldt-Jakob disease.79–82

The Diffusion Tensor

As discussed previously, variations in diffusion-weighted signal intensity due to the anisotropy of white matter tracts can be troublesome for the interpretation of clinical DWI, unless rotationally invariant geometric mean DWI and trace ADC maps are computed. However, the anisotropic diffusion of coherently oriented axonal fibers can also be exploited for quantitative characterization and anatomic mapping of white matter tracts. If at least 6 diffusion-encoded image sets are acquired along noncollinear directions, in addition to at least one b = 0 s/mm2 (or low b) image set, the diffusion tensor can be calculated.32, 83

The diffusion tensor, a 3 × 3 matrix of vectors, is a mathematic model of the 3D pattern of diffusion anisotropy of white matter tracts. The tensor, D, can be related to the diffusion-weighted signal intensity, S, and the b = 0 s/mm2 signal intensity, S0, as follows: Math8)

In this formalism, the diffusion-weighting factor, b, incorporates the direction and magnitude of the applied diffusion gradient vector (Gx, Gy, Gz). Six or more measurements of S by using noncollinear diffusion gradients are necessary to estimate D by using linear regression methods.32, 83

The most intuitive way to conceptualize the information provided by the diffusion tensor is to view it geometrically (Fig 4). The tensor effectively fits the angular variation of the ADC values to the shape of a 3D ellipsoid. The diffusion ellipsoid is a shape defined by 6 variables that describes the ADC of water molecules in each direction at a particular time. For isotropic diffusion, the diffusion ellipsoid is a sphere, because the ADC in every direction is equal. Anisotropic diffusion is modeled with an elongated ellipsoid, indicating a greater mean diffusion distance along the longest axis of the ellipsoid. The elements of the tensor above the diagonal are always equal to those below the diagonal (Fig 4, bottom row), a characteristic termed “conjugate symmetry”, which reflects the antipodal symmetry of Brownian motion. Thus, there are only 6 independent elements of the tensor, necessitating a minimum of 6 noncollinear diffusion-encoding measurements to solve for the tensor elements. The diagonal terms of the tensor indicate the magnitude of diffusivity in each of 3 orthogonal directions. In the case of anisotropic diffusion, the off-diagonal terms of the diffusion tensor indicate the magnitude of diffusion along 1 direction arising from a concentration gradient in an orthogonal direction.

Fig 4.
Fig 4.

The diffusion ellipsoids and tensors for isotropic unrestricted diffusion, isotropic restricted diffusion, and anisotropic restricted diffusion are shown.

Diffusion Tensor Parameters

A number of diffusion tensor metrics are used to characterize the dimensions and shape of the diffusion ellipsoid associated with the microstructure of a particular voxel. The 3 principal axes of the diffusion tensor, termed the “eigenvectors,” can be calculated by diagonalizing the diffusion tensor: Math9)

The diffusion tensor is rotated by matrix R to produce the diagonal matrix, Λ. The columns of R are composed of the eigenvectors of the system, and RT is the matrix transpose of R. The 3 eigenvectors and rotationally invariant eigenvalues λ1, λ2, λ3 describe the directions and lengths of the 3 diffusion ellipsoid axes, respectively, in descending order of magnitude (Fig 5, top row). The largest eigenvector, termed the “primary eigenvector,” and its associated eigenvalue λ1 indicate, respectively, the direction and magnitude of greatest water diffusion. The primary eigenvector is important for fiber tractography algorithms because this vector indicates the orientation of axonal fiber bundles. Therefore, λ1 is also termed “longitudinal diffusivity,” because it specifies the rate of diffusion along the orientation of the fibers. The second and third eigenvectors are orthogonal to the primary eigenvector, and their associated eigenvalues λ2 and λ3 give the magnitude of diffusion in the plane transverse to axonal bundles. Hence, the mean of λ2 and λ3 is also known as “radial diffusivity”.

Fig 5.
Fig 5.

Top row: The first, second, and third eigenvalues are shown with the same intensity scaling. Note that the eigenvalues are always ordered in descending order of intensity with the first eigenvalue being the greatest. Bottom left: The directionally averaged diffusivity is the mean of the 3 eigenvalues. Bottom middle: The FA indicates the coherence of white matter bundles. Bottom right: The FA map can be colorized to show the orientation of the primary eigenvector with left-to-right oriented axonal fibers green, anterior-to-posterior fibers red, and inferior-to-superior fibers blue. Colors are additively mixed to represent fiber populations oriented between these 3 cardinal axes.

A number of additional rotationally invariant diffusion metrics, derived from the 3 eigenvalues, are commonly used to describe the microstructure in a particular voxel. The mean diffusivity (Dav) is the mean of the 3 eigenvalues and describes the directionally averaged diffusivity of water within a voxel: Math10). The trace of D is the sum of the 3 eigenvalues and is another measure of orientationally averaged diffusion. The fractional anisotropy (FA) and relative anisotropy (RA) indices measure the degree of directionality of intravoxel diffusivity: Math11) Math12). FA and RA can both also be defined by equivalent formulas where the numerators are expressed in terms of the difference of each eigenvalue from the mean diffusivity: Math13) Math14).

When the primary eigenvalue is much larger than the second and third eigenvalues, anisotropy measures such as FA and RA will be high, indicating a preferred direction of diffusion. This corresponds to a prolate (cigar) shape of the diffusion ellipsoid (Fig 4, right column), with the preferred direction of diffusion indicated by the long axis of the ellipsoid or, equivalently, by the primary eigenvector of the tensor. In the brain, prolate diffusion within a voxel usually indicates a single coherently organized white matter fiber bundle, with the axonal orientation coincident with the primary eigenvector. FA has become by far the most widely used measure of anisotropy in the DTI literature, and its value varies from zero, in the case of isotropic diffusion, up to a maximum of 1, indicating perfectly linear diffusion occurring only along the primary eigenvector. The fiber orientation information inherent in the primary eigenvector can be visualized on 2D images by assigning a color to each of 3 mutually orthogonal axes,84 typically red to left-right, green to anteroposterior, and blue to up-down (Fig 5, bottom right).

DTI Fiber Tracking: Methodology

The objective of DTI fiber tracking is to determine intervoxel connectivity on the basis of the anisotropic diffusion of water.34–36, 85, 86 The clinical and scientific utility of DTI fiber tracking is found in both the localization and the quantitative assessment of specific neuronal pathways, as applied to basic neuroscience,87 cognitive neuroscience,88, 89 and diagnostic neuroradiology.90–92 In each brain voxel, the dominant direction of axonal tracts can be assumed to be parallel to the primary eigenvector of the diffusion tensor. Fiber tracking uses the diffusion tensor of each voxel to follow an axonal tract in 3D from voxel to voxel through the human brain. Because DTI provides only microstructural information at relatively low spatial resolution, DTI fiber tracking is often combined with functional and/or higher resolution anatomic information to delineate specific pathways.34, 91, 93 In this way, 3D DTI tractography has opened up a whole new dimension to the ability to depict human neuroanatomy noninvasively. This new anatomic connectivity information has been summarized in review articles,94, 95 as well as presented in a book-length DTI atlas.96

DTI fiber tracking algorithms can be divided into deterministic and probabilistic methods. Fiber assignment by continuous tracking (FACT) is a deterministic method, which initiates fiber trajectories from user-defined voxels (Fig 6).35 Fiber trajectories, also known as “streamlines”, follow the primary eigenvector from voxel to voxel in 3 dimensions. When the fiber trajectory reaches the edge of the voxel, the direction of the trajectory is changed to match the primary eigenvector of the next voxel. Constraints on the maximum turning angle of the streamline between voxels and on the minimum FA within a voxel for propagation of the streamline can be applied to contain the fiber tracks to regions of the brain where the diffusion tensor model realistically represents the white matter pathways. Figure 7 shows how user-defined regions of interest, based on prior anatomic knowledge, can be used to restrict fiber tracks to the corticospinal tract.34 This multiple region-of-interest technique for isolating anatomically specific fiber pathways by using DTI tractography has been called “virtual dissection”.97

Fig 6.
Fig 6.

Schematic demonstrating the FACT algorithm. Arrows represent primary eigenvectors in each voxel. Red lines are FACT trajectories.

Fig 7.
Fig 7.

Multiple regions of interest are used with the FACT algorithm to delineate the corticospinal tract. Left: Fiber tracks (red) are generated from a region drawn in the cerebral peduncle (yellow voxels). Middle: Streamlines also passing through a region drawn in the posterior limb of the internal capsule (green voxels) are retained. Right: The final set of streamlines most closely corresponding to the corticospinal tract passes through the centrum semiovale (blue) in addition to the internal capsule and cerebral peduncle regions.

Noise, patient movement, and distortion from imaging artifacts produce uncertainty in the orientation of the diffusion ellipsoid and are detrimental to deterministic streamline fiber tracking.98, 99 Probabilistic fiber tracking methods incorporate the expected uncertainty into the tracking algorithm and can be used to produce a connectivity metric for each voxel. The probability density function of the orientation of a neuronal fiber can be estimated with an empiric function based on the FA,86 a Bayesian model,100 or bootstrap statistics.101 Probabilistic DTI fiber tracking techniques tend to disperse trajectories more than deterministic methods and have the potential to delineate a greater portion of a white matter tract. However, the accuracy of these probabilistic methods is still limited by the information contained in the diffusion tensor and the method of constructing the probability density function. Another fundamental limitation of diffusion tractography is that it cannot distinguish antegrade from retrograde along a fiber pathway, due to the antipodal symmetry inherent to the diffusion process.

DTI Fiber Tracking: Clinical Applications

The visualization of an entire white matter tract in 3D has clinical and scientific value for detecting gross changes to the anatomic course and the microstructural integrity of specific pathways. DTI has recently been used to identify and characterize novel defects in axonal growth and guidance in developmental disorders, such as the absence of normally decussating pontocerebellar fibers in horizontal gaze palsy with progressive scoliosis due to mutation of the ROBO3 gene102 and the ectopic location of pontocerebellar fibers in pontine tegmental cap dysplasia.103 An aberrant fiber pathway known as the “asymmetric sigmoid bundle” was first identified with DTI fiber tracking in individuals with dysgenesis of the corpus callosum.104, 105 Brain tumors and other intracranial mass lesions are capable of dramatically altering the position of the corticospinal tract; hence, knowledge of the location of this important tract within deep white matter is critical for resecting mass lesions without postoperative motor deficit (Fig 8).90–92, 106 DTI fiber tracks can be used in conjunction with stereotactic navigation to identify a safety margin of approximately 1 cm around the motor tract, which can be used for surgical planning.107, 108

Fig 8.
Fig 8.

DTI fiber tracks reveal the course of the corticospinal tract along the border of a brain tumor (blue). Streamlines were launched from wrist (green) and shoulder (red) motor stimulation sites on the cortex. The wrist and shoulder motor streamlines twist about each other as they descend from the cortex through the internal capsule to the cerebral peduncle.

In addition to basic 3D visualization, many studies have used fiber tracking to delineate specific white matter tracts for quantitative analysis. Quantitative DTI tractography studies have examined the microstructure of white matter tracts in pediatric subjects,109–112 in elderly subjects,113 and in patients with schizophrenia,114 brain tumors,115 Alzheimer disease,116 and many other disorders. DTI fiber tracking can objectively create 3D regions of interest specific to an entire white matter tract. However, most white matter tracts have heterogeneous structural characteristics, and fiber tracking can be used to segment a pathway into several regions for quantitative analysis. Figure 9 shows the optic radiations in a premature infant color-coded according to the underlying FA values in the voxels contained within the tracts. The anterior portion of the optic radiation adjacent to the thalamus was observed to have significantly higher FA than the posterior portions of the tract.117 The spatial and temporal heterogeneity of DTI metrics has also been observed with fiber tracking of sensorimotor tracts in premature infants, indicating the maturation of the delineated tract and the emergence of other tracts crossing the sensorimotor pathway in the centrum semiovale.111

Fig 9.
Fig 9.

DTI fiber tracks of the optic radiation in a 35-week gestational age premature infant. Streamlines were generated with the FACT algorithm and are colored according to the underlying FA in the voxels that the streamlines pass through. The proximal segment of the optic radiations, near the lateral geniculate nucleus, has the highest anisotropy.

Conclusion

This review article has explored the theoretic background needed to understand clinical DWI and DTI, including fiber tractography, and their application to neuroradiology. These diffusion MR imaging techniques provide microstructural information about biologic tissues that is not available from other imaging techniques. In the central nervous system, this has yielded important new tools for diagnosis in ischemia, infection, tumors, and demyelinating disease, among other pathologies, as well as for presurgical mapping of white matter pathways to avoid postoperative injury.

However, even as sophisticated a mathematic construct as the diffusion tensor is an oversimplification of the properties of water diffusion in the brain. The limitations of the diffusion tensor in areas of complex white matter architecture, where fiber tracts intersect, branch, or are otherwise partial volume averaged within a voxel, affect the ability of DTI fiber tractography to fully delineate an axonal pathway and may also lead to the generation of spurious tracks.95 Measurements of quantitative DTI parameters such as FA are also difficult or impossible to interpret in regions of complex white matter. These problems have led to the introduction of more advanced methods such as high angular resolution diffusion imaging118–120 and diffusion spectrum imaging,121 which promise to overcome many of the inadequacies of the tensor model. These newer methods take better advantage of ongoing technical developments, including the synergistic combination of ultra-high field diffusion122 with highly accelerated parallel imaging,123–125 and lead to new scientific and clinical applications such as probabilistic tractography126–128 and whole-brain connectivity networks.129 Hence, these newer techniques that transcend the diffusion tensor are likely to be adopted in clinical neuroradiology during the years to come.

References

  1. ↵
    Einstein A. Investigations on the Theory of the Brownian Movement. New York: Dover;1956
  2. ↵
    Le Bihan D, Breton E, Lallemand D, et al. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 1986;161:401–07
    CrossRefPubMed
  3. Le Bihan D, Breton E, Lallemand D, et al. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988;168:497–505
    PubMed
  4. ↵
    Thomsen C, Henriksen O, Ring P. In vivo measurement of water self diffusion in the human brain by magnetic resonance imaging. Acta Radiol 1987;28:353–61
    PubMed
  5. ↵
    Turner R, Le Bihan D, Maier J, et al. Echo-planar imaging of intravoxel incoherent motion. Radiology 1990;177:407–14
    PubMed
  6. ↵
    Moseley ME, Cohen Y, Mintorovitch J, et al. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magn Reson Med 1990;14:330–46
    CrossRefPubMed
  7. Chien D, Kwong KK, Gress DR, et al. MR diffusion imaging of cerebral infarction in humans. AJNR Am J Neuroradiol 1992;13:1097–102, discussion 1103–05
    Abstract/FREE Full Text
  8. Warach S, Chien D, Li W, et al. Fast magnetic resonance diffusion-weighted imaging of acute human stroke. Neurology 1992;42:1717–23. Erratum in: Neurology 1992;42:2192
    FREE Full Text
  9. Marks MP, De Crespigny A, Lentz D, et al. Acute and chronic stroke: navigated spin-echo diffusion-weighted MR imaging. Radiology 1996;199:403–08
    PubMed
  10. ↵
    Gonzalez RG, Schaefer PW, Buonanno FS, et al. Diffusion-weighted MR imaging: diagnostic accuracy in patients imaged within 6 hours of stroke symptom onset. Radiology 1999;210:155–62
    CrossRefPubMed
  11. ↵
    Ebisu T, Naruse S, Horikawa Y, et al. Discrimination between different types of white matter edema with diffusion-weighted MR imaging. J Magn Reson Imaging 1993;3:863–68
    PubMed
  12. Schaefer PW, Buonanno FS, Gonzalez RG, et al. Diffusion-weighted imaging discriminates between cytotoxic and vasogenic edema in a patient with eclampsia. Stroke 1997;28:1082–85
    Abstract/FREE Full Text
  13. Schwartz R, Mulkern R, Gudbjartsson H, et al. Diffusion-weighted MR imaging in hypertensive encephalopathy: clues to pathogenesis. AJNR Am J Neuroradiol 1998;19:859–62
    Abstract
  14. Ay H, Buonanno FS, Schaefer PW, et al. Posterior leukoencephalopathy without severe hypertension: utility of diffusion-weighted MRI. Neurology. 1998;51:1369–76
    Abstract/FREE Full Text
  15. Mukherjee P, McKinstry RC. Reversible posterior leukoencephalopathy syndrome: evaluation with diffusion-tensor MR imaging. Radiology 2001;219:756–65
    CrossRefPubMed
  16. ↵
    Provenzale JM, Petrella JR, Cruz LCH Jr, et al. Quantitative assessment of diffusion abnormalities in posterior reversible encephalopathy syndrome. AJNR Am J Neuroradiol. 2001;22:1455–61
    Abstract/FREE Full Text
  17. ↵
    Arfanakis K, Haughton VM, Carew JD, et al. Diffusion tensor MR imaging in diffuse axonal injury. AJNR Am J Neuroradiol. 2002;23:794–802
    Abstract/FREE Full Text
  18. Hergan K, Schaefer PW, Sorensen AG, et al. Diffusion-weighted MRI in diffuse axonal injury of the brain. Eur Radiol 2002;12:2536–41
    CrossRefPubMed
  19. ↵
    Huisman TA, Sorensen AG, Hergan K, et al. Diffusion-weighted imaging for the evaluation of diffuse axonal injury in closed head injury. J Comput Assist Tomogr 2003;27:5–11
    CrossRefPubMed
  20. ↵
    Tien R, Felseberg G, Friedman H, et al. MR imaging of high-grade cerebral gliomas: value of diffusion-weighted echoplanar pulse sequences. AJR Am J Roentgenol 1994;162:671–77
    PubMed
  21. Brunberg J, Chenevert T, McKeever P, et al. In vivo MR determination of water diffusion coefficients and diffusion anisotropy: correlation with structural alteration in gliomas of the cerebral hemispheres. AJNR Am J Neuroradiol. 1995;16:361–71
    Abstract/FREE Full Text
  22. ↵
    Krabbe K, Gideon P, Wagn P, et al. MR diffusion imaging of human intracranial tumours. Neuroradiology 1997;39:483–89
    CrossRefPubMed
  23. ↵
    Gauvain KM, McKinstry RC, Mukherjee P, et al. Evaluating pediatric brain tumor cellularity with diffusion-tensor imaging. AJR Am J Roentgenol 2001;177:449–54
    CrossRefPubMed
  24. Kono K, Inoue Y, Nakayama K, et al. The role of diffusion-weighted imaging in patients with brain tumors. AJNR Am J Neuroradiol 2001;22:1081–88
    Abstract/FREE Full Text
  25. ↵
    Guo AC, Cummings TJ, Dash RC, et al. Lymphomas and high-grade astrocytomas: comparison of water diffusibility and histologic characteristics. Radiology 2002;224:177–83
    CrossRefPubMed
  26. Chenevert TL, Sundgren PC, Ross BD. Diffusion imaging: insight to cell status and cytoarchitecture. Neuroimaging Clin N Am 2006;16:619–32
    CrossRefPubMed
  27. ↵
    Lu S, Ahn D, Johnson G, et al. Peritumoral diffusion tensor imaging of high-grade gliomas and metastatic brain tumors. AJNR Am J Neuroradiol 2003;24:937–41
    Abstract/FREE Full Text
  28. ↵
    Smith JS, Cha S, Mayo MC, et al. Serial diffusion-weighted magnetic resonance imaging in cases of glioma: distinguishing tumor recurrence from postresection injury. J Neurosurg 2005;103:428–38
    CrossRefPubMed
  29. ↵
    Ebisu T, Tanaka C, Umeda M, et al. Discrimination of brain abscess from necrotic or cystic tumors by diffusion-weighted echo planar imaging. Magn Reson Imaging 1996;14:1113–16
    CrossRefPubMed
  30. ↵
    Kim Y, Chang K, Kim H, et al. Brain abscess and necrotic or cystic brain tumor: discrimination with signal intensity on diffusion-weighted MR imaging. AJR Am J Roentgenol 1998;171:1487–90
    CrossRefPubMed
  31. ↵
    Leuthardt EC, Wippold FJ 2nd, Oswood MC, et al. Diffusion-weighted MR imaging in the preoperative assessment of brain abscesses. Surg Neurol 2002;58:395–402
    CrossRefPubMed
  32. ↵
    Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion-tensor from the NMR spin echo. J Magn Reson B 1994;103:247–54
    CrossRefPubMed
  33. ↵
    Pierpaoli C, Jezzard P, Basser PJ, et al. Diffusion tensor MR imaging of the human brain. Radiology 1996;201:637–48
    PubMed
  34. ↵
    Conturo TE, Lori NF, Cull TS, et al. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci U S A 1999;96:10422–27
    Abstract/FREE Full Text
  35. ↵
    Mori S, Kaufmann WE, Pearlson GD, et al. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 1999;45:265–69
    CrossRefPubMed
  36. ↵
    Basser PJ, Pajevic S, Pierpaoli C, et al. In vivo fiber tractography using DT-MRI data. Magn Reson Med 2000;44:625–32
    CrossRefPubMed
  37. ↵
    Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys 1965;42:288–92
    CrossRef
  38. ↵
    Huppi PS, Maier SE, Peled S, et al. Microstructural development of human newborn cerebral white matter assessed in vivo by diffusion tensor magnetic resonance imaging. Pediatr Res 1998;44:584–90
    CrossRefPubMed
  39. ↵
    Neil JJ, Shiran SI, McKinstry RC, et al. Normal brain in human newborns: apparent diffusion coefficient and diffusion anisotropy measured by using diffusion tensor MR imaging. Radiology 1998;209:57–66
    PubMed
  40. ↵
    DeLano MC, Cao Y. High b-value diffusion imaging. Neuroimaging Clin N Am 2002;12:21–34
    CrossRefPubMed
  41. ↵
    Kim HJ, Choi CG, Lee DH, et al. High-b-value diffusion-weighted MR imaging of hyperacute ischemic stroke at 1.5T. AJNR Am J Neuroradiol 2005;26:208–15
    Abstract/FREE Full Text
  42. ↵
    Chen PE, Simon JE, Hill MD, et al. Acute ischemic stroke: accuracy of diffusion-weighted MR imaging—effects of b value and cerebrospinal fluid suppression. Radiology 2006;238:232–39
    PubMed
  43. ↵
    Maldjian JA, Listerud J, Moonis G, et al. Computing diffusion rates in T2-dark hematomas and areas of low T2 signal. AJNR Am J Neuroradiol 2001;22:112–18
    Abstract/FREE Full Text
  44. ↵
    Mulkern RV, Gudbjartsson H, Westin CF, et al. Multi-component apparent diffusion coefficients in human brain. NMR Biomed 1999;12:51–62
    CrossRefPubMed
  45. ↵
    Mulkern RV, Vajapeyam S, Robertson RL, et al. Biexponential apparent diffusion coefficient parameterization in adult vs newborn brain. Magn Reson Imaging 2001;19:659–68
    CrossRefPubMed
  46. ↵
    Provenzale JM, Engelter ST, Petrella JR, et al. Use of MR exponential diffusion-weighted images to eradicate T2 “shine-through” effect. AJR Am J Roentgenol 1999;172:537–39
    PubMed
  47. ↵
    Shimony JS, McKinstry RC, Akbudak E, et al. Quantitative diffusion-tensor anisotropy brain MR imaging: normative human data and anatomic analysis. Radiology 1999;212:770–84
    PubMed
  48. ↵
    Sorensen AG, Wu O, Copen WA, et al. Human acute cerebral ischemia: detection of changes in water diffusion anisotropy by using MR imaging. Radiology 1999;212:785–92
    CrossRefPubMed
  49. ↵
    Chenevert TL, Brunberg JA, Pipe JG. Anisotropic diffusion in human white matter: demonstration with MR techniques in vivo. Radiology 1990;177:401–05
    PubMed
  50. ↵
    Mukherjee P, Miller JH, Shimony JS, et al. Normal brain maturation during childhood: developmental trends characterized with diffusion-tensor MR imaging. Radiology 2001;221:349–58
    CrossRefPubMed
  51. ↵
    Mukherjee P, McKinstry RC. Diffusion tensor imaging and tractography of human brain development. Neuroimaging Clin N Am 2006;16:19–43
    CrossRefPubMed
  52. Mukherjee P, Miller JH, Shimony JS, et al. Diffusion-tensor MR imaging of gray and white matter development during normal human brain maturation. AJNR Am J Neuroradiol 2002;23:1445–56
    Abstract/FREE Full Text
  53. McGraw P, Liang L, Provenzale JM. Evaluation of normal age-related changes in anisotropy during infancy and childhood as shown by diffusion tensor imaging. AJR Am J Roentgenol 2002;179:1515–22
    PubMed
  54. Schneider JF, Il'yasov KA, Hennig J, et al. Fast quantitative diffusion-tensor imaging of cerebral white matter from the neonatal period to adolescence. Neuroradiology 2004;46:258–66
    CrossRefPubMed
  55. Snook L, Paulson LA, Roy D, et al. Diffusion tensor imaging of neurodevelopment in children and young adults. Neuroimage 2005;26:1164–73
    CrossRefPubMed
  56. ↵
    Hermoye L, Saint-Martin C, Cosnard G, et al. Pediatric diffusion tensor imaging: normal database and observation of the white matter maturation in early childhood. Neuroimage 2006;29:493–504
    CrossRefPubMed
  57. ↵
    Gideon P, Thomsen C, Henriksen O. Increased self-diffusion of brain water in normal aging. J Magn Reson Imaging 1994;4:185–88
    PubMed
  58. Chun T, Filippi CG, Zimmerman RD, et al. Diffusion changes in the aging human brain. AJNR Am J Neuroradiol 2000;21:1078–83
    Abstract/FREE Full Text
  59. Engelter ST, Provenzale JM, Petrella JR, et al. The effect of aging on the apparent diffusion coefficient of normal-appearing white matter. AJR Am J Roentgenol 2000;175:425–30
    PubMed
  60. Chen ZG, Li TQ, Hindmarsh T. Diffusion tensor trace mapping in normal adult brain using single-shot EPI technique: a methodological study of the aging brain. Acta Radiol 2001;42:447–558
    FREE Full Text
  61. Nusbaum AO, Tang CY, Buchsbaum MS, et al. Regional and global changes in cerebral diffusion with normal aging. AJNR Am J Neuroradiol 2001;22:136–42
    Abstract/FREE Full Text
  62. ↵
    Moseley ME. Diffusion tensor imaging and aging: a review. NMR Biomed 2002;15:553–60
    CrossRefPubMed
  63. ↵
    Sotak CH. Nuclear magnetic resonance (NMR) measurement of the apparent diffusion coefficient (ADC) of tissue water and its relationship to cell volume changes in pathological states. Neurochem Int 2004;45:569–82
    CrossRefPubMed
  64. ↵
    Duong TQ, Ackerman JJ, Ying HS, et al. Evaluation of extra- and intracellular apparent diffusion in normal and globally ischemic rat brain via 19F NMR. Magn Reson Med 1998;40:1–13
    PubMed
  65. ↵
    Mishra AM, Gupta RK, Saksena S, et al. Biological correlates of diffusivity in brain abscess. Magn Reson Med 2005;54:878–85
    CrossRefPubMed
  66. ↵
    Tsuchiya K, Osawa A, Katase S, et al. Diffusion-weighted MRI of subdural and epidural empyemas. Neuroradiology 2003;45:220–23
    CrossRefPubMed
  67. ↵
    Pezzullo JA, Tung GA, Mudigonda S, et al. Diffusion-weighted MR imaging of pyogenic ventriculitis. AJR Am J Roentgenol 2003;180:71–75
    PubMed
  68. ↵
    Tsuruda JS, Chew WM, Moseley ME, et al. Diffusion-weighted MR imaging of the brain: value of differentiating between extraaxial cysts and epidermoid tumors. AJNR Am J Neuroradiol 1990;11:925–31, discussion 932–34
    Abstract/FREE Full Text
  69. ↵
    Tsuruda JS, Chew WM, Moseley ME, et al. Diffusion-weighted MR imaging of extraaxial tumors. Magn Reson Med 1991;19:316–20
    PubMed
  70. ↵
    Uhl M, Altehoefer C, Kontny U, et al. MRI-diffusion imaging of neuroblastomas: first results and correlation to histology. Eur Radiol 2002;12:2335–38. Epub 2002 Mar 19
    PubMed
  71. ↵
    Erdem E, Zimmerman RA, Haselgrove JC, et al. Diffusion-weighted imaging and fluid attenuated inversion recovery imaging in the evaluation of primitive neuroectodermal tumors. Neuroradiology 2001;43:927–33
    CrossRefPubMed
  72. ↵
    Hartmann M, Jansen O, Heiland S, et al. Restricted diffusion within ring enhancement is not pathognomonic for brain abscess. AJNR Am J Neuroradiol 2001;22:1738–42
    Abstract/FREE Full Text
  73. ↵
    Mader I, Wolff M, Niemann G, et al. Acute haemorrhagic encephalomyelitis (AHEM): MRI findings. Neuropediatrics 2004;35:143–46
    CrossRefPubMed
  74. ↵
    Sagar P, Grant PE. Diffusion-weighted MR imaging: pediatric clinical applications. Neuroimaging Clin N Am 2006;16:45–74
    CrossRefPubMed
  75. ↵
    Sener RN. Diffusion magnetic resonance imaging patterns in metabolic and toxic brain disorders. Acta Radiol 2004;45:561–70
    CrossRefPubMed
  76. ↵
    Teksam M, Casey SO, Michel E, et al. Diffusion-weighted MR imaging findings in carbon monoxide poisoning. Neuroradiology 2002;44:109–13
    CrossRefPubMed
  77. Sandoval C, Kutscher M, Jayabose S, et al. Neurotoxicity of intrathecal methotrexate: MR imaging findings. AJNR Am J Neuroradiol 2003;24:1887–90
    Abstract/FREE Full Text
  78. ↵
    McKinney AM, Filice RW, Teksam M, et al. Diffusion abnormalities of the globi pallidi in manganese neurotoxicity. Neuroradiology 2004;46:291–95
    CrossRefPubMed
  79. ↵
    Bahn M, Kido D, Lin W, et al. Brain magnetic resonance diffusion abnormalities in Creutzfeldt-Jakob disease. Arch Neurol 1997;54:1411–15
    CrossRefPubMed
  80. Demaerel P, Baert AL, Vanopdenbosch L, et al. Diffusion-weighted magnetic resonance imaging in Creutzfeldt-Jakob disease. Lancet 1997;349:847–48
    PubMed
  81. Bahn MM, Parchi P. Abnormal diffusion-weighted magnetic resonance images in Creutzfeldt-Jakob disease. Arch Neurol 1999;56:577–83
    CrossRefPubMed
  82. ↵
    Demaerel P, Heiner L, Robberecht W, et al. Diffusion-weighted MRI in sporadic Creutzfeldt-Jakob disease. Neurology 1999;52:205–08
    Abstract/FREE Full Text
  83. ↵
    Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 1994;66:259–67
    CrossRefPubMed
  84. ↵
    Pajevic S, Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn Reson Med 1999;42:526–40. Erratum in: Magn Reson Med 2000;43:921
    CrossRefPubMed
  85. ↵
    Gossl C, Fahrmeir L, Putz B, et al. Fiber tracking from DTI using linear state space models: detectability of the pyramidal tract. Neuroimage 2002;16:378–88
    CrossRefPubMed
  86. ↵
    Parker GJ, Haroon HA, Wheeler-Kingshott CA. A framework for a streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. J Magn Reson Imaging 2003;18:242–54
    CrossRefPubMed
  87. ↵
    Mori S, Zhang J. Principles of diffusion tensor imaging and its applications to basic neuroscience research. Neuron 2006;51:527–39
    CrossRefPubMed
  88. ↵
    ffytche DH, Catani M. Beyond localization: from hodology to function. Philos Trans R Soc Lond B Biol Sci 2005;360:767–79
    Abstract/FREE Full Text
  89. ↵
    Catani M. Diffusion tensor magnetic resonance imaging tractography in cognitive disorders. Curr Opin Neurol 2006;19:599–606
    PubMed
  90. ↵
    Holodny AI, Schwartz TH, Ollenschleger M, et al. Tumor involvement of the corticospinal tract: diffusion magnetic resonance tractography with intraoperative correlation. J Neurosurg 2001;95:1082
    PubMed
  91. ↵
    Berman JI, Berger MS, Mukherjee P, et al. Diffusion-tensor imaging-guided tracking of fibers of the pyramidal tract combined with intraoperative cortical stimulation mapping in patients with gliomas. J Neurosurg 2004;101:66–72
    PubMed
  92. ↵
    Nimsky C, Ganslandt O, Hastreiter P, et al. Preoperative and intraoperative diffusion tensor imaging-based fiber tracking in glioma surgery. Neurosurgery 2005;56:130–37
    PubMed
  93. ↵
    Guye M, Parker GJ, Symms M, et al. Combined functional MRI and tractography to demonstrate the connectivity of the human primary motor cortex in vivo. Neuroimage 2003;19:1349–60
    CrossRefPubMed
  94. ↵
    Wakana S, Jiang H, Nagae-Poetscher LM, et al. Fiber tract-based atlas of human white matter. Radiology 2004;230:77–87
    CrossRefPubMed
  95. ↵
    Hess CP, Mukherjee P. Visualizing white matter pathways in the living human brain: diffusion tensor imaging and beyond. Neuroimaging Clin N Am 2007;17:407–26
    CrossRefPubMed
  96. ↵
    Mori S, Wakana S, Nagae-Poetscher LM, et al. MRI Atlas of Human White Matter. Amsterdam: Elsevier;2005
  97. ↵
    Catani M, Howard RJ, Pajevic S, et al. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage 2002;17:77–94
    CrossRefPubMed
  98. ↵
    Anderson AW. Theoretical analysis of the effects of noise on diffusion tensor imaging. Magn Reson Med 2001;46:1174–88
    CrossRefPubMed
  99. ↵
    Lazar M, Alexander AL. An error analysis of white matter tractography methods: synthetic diffusion tensor field simulations. Neuroimage 2003;20:1140–53
    CrossRefPubMed
  100. ↵
    Behrens TE, Woolrich MW, Jenkinson M, et al. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med 2003;50:1077–88
    CrossRefPubMed
  101. ↵
    Lazar M, Alexander AL. Bootstrap white matter tractography (BOOT-TRAC). Neuroimage 2005;24:524–32. Epub 2004 Nov 24
    CrossRefPubMed
  102. ↵
    Sicotte NL, Salamon G, Shattuck DW, et al. Diffusion tensor MRI shows abnormal brainstem crossing fibers associated with ROBO3 mutations. Neurology 2006;67:519–21
    Abstract/FREE Full Text
  103. ↵
    Barth PG, Majoie CB, Caan MW, et al. Pontine tegmental cap dysplasia: a novel brain malformation with a defect in axonal guidance. Brain 2007;130 (Pt 9):2258–66. Epub 2007 Aug 9
  104. ↵
    Tovar-Moll F, Moll J, de Oliveira-Souza R, et al. Neuroplasticity in human callosal dysgenesis: a diffusion tensor imaging study. Cereb Cortex 2007;17:531–41
    Abstract/FREE Full Text
  105. ↵
    Paul LK, Brown WS, Adolphs R, et al. Agenesis of the corpus callosum: genetic, developmental and functional aspects of connectivity. Nat Rev Neurosci 2007;8:287–99
    CrossRefPubMed
  106. ↵
    Hendler T, Pianka P, Sigal M, et al. Delineating gray and white matter involvement in brain lesions: three-dimensional alignment of functional magnetic resonance and diffusion-tensor imaging. J Neurosurg 2003;99:1018–27
    PubMed
  107. ↵
    Bello L, Gambini A, Castellano A, et al. Motor and language DTI fiber tracking combined with intraoperative subcortical mapping for surgical removal of gliomas. Neuroimage 2008;39:369–82. Epub 2007 Aug 29
    CrossRefPubMed
  108. ↵
    Berman JI, Berger MS, Chung SW, et al. Accuracy of diffusion tensor magnetic resonance imaging tractography assessed using intraoperative subcortical stimulation mapping and magnetic source imaging. J Neurosurg 2007;107:488–94
    CrossRefPubMed
  109. ↵
    Glenn OA, Henry RG, Berman JI, et al. DTI-based three-dimensional tractography detects differences in the pyramidal tracts of infants and children with congenital hemiparesis. J Magn Reson Imaging 2003;18:641–48
    CrossRefPubMed
  110. Partridge SC, Mukherjee P, Berman JI, et al. Tractography-based quantitation of diffusion tensor imaging parameters in white matter tracts of preterm newborns. J Magn Reson Imaging 2005;22:467–74
    CrossRefPubMed
  111. ↵
    Berman JI, Mukherjee P, Partridge SC, et al. Quantitative diffusion tensor MRI fiber tractography of sensorimotor white matter development in premature infants. Neuroimage 2005;27:862–71
    CrossRefPubMed
  112. ↵
    Dubois J, Hertz-Pannier L, Dehaene-Lambertz G, et al. Assessment of the early organization and maturation of infants' cerebral white matter fiber bundles: a feasibility study using quantitative diffusion tensor imaging and tractography. Neuroimage 2006;30:1121–32
    CrossRefPubMed
  113. ↵
    Sullivan EV, Adalsteinsson E, Pfefferbaum A. Selective age-related degradation of anterior callosal fiber bundles quantified in vivo with fiber tracking. Cereb Cortex 2006;16:1030–39
    Abstract/FREE Full Text
  114. ↵
    Jones DK, Catani M, Pierpaoli C, et al. Age effects on diffusion tensor magnetic resonance imaging tractography measures of frontal cortex connections in schizophrenia. Hum Brain Mapp 2006;27:230–38
    CrossRefPubMed
  115. ↵
    Roberts TP, Liu F, Kassner A, et al. Fiber density index correlates with reduced fractional anisotropy in white matter of patients with glioblastoma. AJNR Am J Neuroradiol 2005;26:2183–86
    Abstract/FREE Full Text
  116. ↵
    Taoka T, Iwasaki S, Sakamoto M, et al. Diffusion anisotropy and diffusivity of white matter tracts within the temporal stem in Alzheimer disease: evaluation of the “tract of interest” by diffusion tensor tractography. AJNR Am J Neuroradiol 2006;27:1040–45
    Abstract/FREE Full Text
  117. ↵
    Berman JI, Glass HC, Miller SP, et al. Quantitative Fiber Tracking Analysis of the Optic Radiations in Premature Newborns. Proceedings of the Fifteenth Annual Meeting of the International Society of Magnetic Resonance in Medicine, Berlin, Germany, May 19-25,2007
  118. ↵
    Tuch DS, Reese TG, Wiegell MR, et al. Diffusion MRI of complex neural architecture. Neuron2003;40:885–95
  119. Tournier JD, Calamante F, Gadian DG, et al. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage 2004;23:1176–85
    CrossRefPubMed
  120. ↵
    Hess CP, Mukherjee P, Han ET, et al. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn Reson Med 2006;56:104–17
    CrossRefPubMed
  121. ↵
    Wedeen VJ, Hagmann P, Tseng WY, et al. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 2005;54:1377–86
    CrossRefPubMed
  122. ↵
    Mukherjee P, Hess CP, Xu D, et al. Development and initial evaluation of 7-T q-ball imaging of the human brain. Magn Reson Imaging 2008;26:171–80. Epub 2007 Aug 9
    CrossRefPubMed
  123. ↵
    Ohliger MA, Grant AK, Sodickson DK. Ultimate intrinsic signal-to-noise ratio for parallel MRI: electromagnetic field considerations. Magn Reson Med 2003;50:1018–30
    CrossRefPubMed
  124. Wiesinger F, Van de Moortele PF, Adriany G, et al. Parallel imaging performance as a function of field strength: an experimental investigation using electrodynamic scaling. Magn Reson Med 2004;52:953–64
    CrossRefPubMed
  125. ↵
    Wiesinger F, Van de Moortele PF, Adriany G, et al. Potential and feasibility of parallel MRI at high field. NMR Biomed 2006;19:368–78
    CrossRefPubMed
  126. ↵
    Behrens TE, Berg HJ, Jbabdi S, et al. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 2007;34:144–55. Epub 2006 Oct 27
    CrossRefPubMed
  127. Dyrby TB, Søgaard LV, Parker GJ, et al. Validation of in vitro probabilistic tractography. Neuroimage 2007;37:1267–77
    CrossRefPubMed
  128. ↵
    Berman JI, Chung S, Mukherjee P, et al. Probabilistic streamline q-ball tractography using the residual bootstrap. Neuroimage 2008;39:215–22
    CrossRefPubMed
  129. ↵
    Hagmann P, Kurant M, Gigandet X, et al. Mapping human whole-brain structural networks with diffusion MRI. PLoS ONE 2007;2:e597
    CrossRef
View Abstract
Back to top

In this issue

Advertisement
Print
Download PDF
Email Article
Cite this article
0 Responses
Respond to this article
Bookmark this article
Diffusion Tensor MR Imaging and Fiber Tractography: Theoretic Underpinnings
P. Mukherjee, J.I. Berman, S.W. Chung, C.P. Hess, R.G. Henry
American Journal of Neuroradiology Apr 2008, 29 (4) 632-641; DOI: 10.3174/ajnr.A1051
del.icio.us logo Twitter logo Facebook logo Mendeley logo
Purchase

Jump to section

Related Articles

  • No related articles found.

Cited By...

More in this TOC Section

Similar Articles

Advertisement